「統計的に有意である」ことを証明する!平均値に差があるかを調べるカンタン技法「t検定」【やさしい統計学14】
ビジネスパーソンのためのやさしい統計学「第14回目」
※YouTubeにて各シリーズ連載中
ビジネスパーソンのためのやさしい統計。
今日は徹底的に”やさしく”いきたいと思います。平均値に差があるかどうか、統計的に検証する。「統計的に有意」とか学者やデータアナリストがいうやつです。
ABテストで効果を検証するときに使える「t検定」
今回は、俗にABテストと言われるものを扱います。「広告A・広告B、2種類のWeb広告を打ちました。どっちの方が効果あったでしょう」といった検証。この検証の背後にある『t検定』というものを理論的に、なるべく簡単に説明したうえで、皆さんへの使い方の指南をやっていきたいと思います。

言っても広告だけじゃないです。この2種類のデータを比較するって、ビジネスで、非常に多くのシーンがあると思うので、どうか皆さんの武器に変えていただきたいと願います。
たとえば、農業の生産現場なんかで、新しくできた肥料を試すとき。この肥料を使ったと時と使わなかった時で、野菜の収穫量差がありますか?とか。
はたまたマーケティング施策を考えるにあたって、横浜店と川崎店で客単価に違いがあるかどうか。それに合わせて、メニューとか変えればいいわけですからね。
あるいは、教育業で、オンラインでやる事業とリアルである授業で効果は違ってくるのか。
こういうことって、全部、皆さんのビジネスを成り立たせる上でとても大切なことですよね。
これらの差があるかどうかを科学的に厳密に検証できるのが『t検定』であるとしたならば、私としては、皆さんに学んでいただき、ビジネス力に変えていただきたいと思うのです。この点強調しておきますが、学んでしまえば、皆さん1分とかからずできるわけですから、ぜひともこの記事を最後まで見ていただきたいところです。
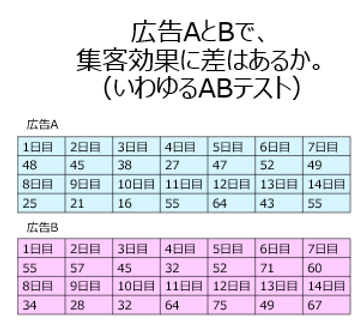
今回の例は上図です。2種類の広告をそれぞれ2週間打ってみました。それぞれ、このくらい集客できました、という図です。
こんにち、こうしたABテストみたいな広告効果のチェックは非常に簡単になっています。なんならこの広告Aも広告Bも、YouTubeで出せばせいぜい1件数円ですし、どんな方法で出したとしても数十円~数百円なんです。なので、どっちの方がいいのだろう?と迷ったら、両方作って検証してみることです。
パッと見て、Bの方が集客できていそうな感じがあったとしても、本当にこの差があるのかどうか皆さんまだ確証を持てないはずです。もし、あと2週間追加的に調査をしたら、実は広告Aの方が効果があった、という可能性も否定できない。
そういうときに、果たしてこの二つの広告の間の差というのは信頼がおけるかどうか、統計的に検証してみようという話になってくるわけなんです。その時に使うのが『t検定』です。
t検定の考え方

もし皆さんがこの広告A広告Bどっちの方が効果あるだろうか?というのを、パッと見て検証しようと思ったら、平均値を見ると思うんですね。
実際、このデータで平均値を取ってみると、広告Aが平均41.8、広告Bが51.5で、その間に10の差があるわけです。これで納得してくれる人も少なくないかもしれない。でも、役員会だとか、会社の中の企画会議で突き出して、『10も差があるじゃないですか!だからBの方がいいんです』と言ったとしても、本当にそうなの?という説得材料としては欠けるわけですよね。
この説得材料となってくるのが、『t検定』なんです。こういう差が得られる確率って、どんな確率なのよ?をはじき出すんです。正確には、単なる偶然である確率を出せる。企画会議などで、今回の結果が偶然だっていうのは、せいぜい5%しかないんですよ、と申し添えることができたら、あなたの言葉の説得力も、もっと上がってくるじゃないですか。
t検定、考え出した人は本当に天才の所業だなと思うわけなんですけれども、でも凡人たる私達も、勉強してしまえば、誰でも使えるようになるのです。これが科学の力です。科学というのは、天才が発明した所業というのを、私達が学べば、誰しも使えるようにできるもの。
しかし『t検定』といっても、別に皆さん中身の数学的な根拠や統計学的な根拠の部分は一先ず分からなくていいです。直感的にどういうことをやっているのかさえ、ここでは分かっておけばいいです。
その広告A広告B2つの数字を取りました。「この2つのサンプル群の平均値の差がある」ってどういうときに言えますか?
第1のポイントは、平均値の差が十分に大きいこと。片方の広告のクリック率が30%、もう片方のクリック率が1%だと言ったら、もう言わずもがなですよね。ということで、まずこの平均値の差が十分に大きい、というのが第1条件だと。
第2条件は、ばらつきが大きいかどうかです。例えば、先ほどの広告のクリック数で、「ある日は何千件とクリックされるけど、ある日はほとんどゼロに近い」という、バラつきが大きいとしたら、どういうことになるでしょうか。ここまで14日間とったけども、15日目、16日目、17日目でも、めちゃくちゃバラつくわけですよね。
それによって平均値も変わってくるのだとすると、このバラつきが小さければ小さいほど、今得られている平均値に信頼がおけることになるじゃないですか。ここでは実際、標準偏差という値を使うことになります。
そして第3にはサンプルが十分に多いことです。3件のデータを取って平均100ですって言われても、皆さん全然信じられないですね。でも3,000件のデータを取った平均が100ですとなれば、100なんだろう、と皆さん納得がされると思うんです。
これらの3つの条件を使うと、「t値」という値を作ることができる。このt値を用いて、得られた平均値の差が偶然かどうかを検証するのが『t検定』です。
3つの性質を利用する
t検定では、以下のような式でt値を算出します。

皆さんにとっては、別にこの式の数学的な根拠なんていうのは、あまり大切ではありません。もし学びたいと思ったら、ぜひそれはとても素晴らしいことなので、ぜひ統計学の教科書とか、もっと専門的に書いているWebサイトを見てください。
差し当たってビジネスで使うにあたっては、直感的に理解すれば問題ありません。このt値という値が、平均の差が大きければ大きいほど数字が大きくなり、データの散らばりが小さければ小さいほど、そしてサンプル数が増えるほど、t値はやっぱり大きくなる。
条件が揃えば揃うほど、t値は大きい数字になっていくということがわかるかと思います。
このt値が例えば3という数値を得られたとして、そこから、この差が偶然的に生じる確率が何%です、という結果が得られるわけなのです。マジですごい研究だと思うんですけど、本当これを発見したゴセットさんとフィッシャーさんマジで偉いし、もう大尊敬であります。でも私達はその天才の所業をエクセル関数で使えばいいんです。1分かからず偶然の結果である確率が得られる。
計算はExcelでできる
今日はめちゃくちゃいい時代でして、これをエクセルでできちゃうんです。もうマイクロソフトさんに感謝です。

しかも本当に難しいことに、何もしなくていいんです。この検定した範囲をドラッグするだけでこれで出来ちゃうんです。とはいえ、関数名は知っておかないとですね!関数の名前はt検定ということでそのまんま、t.test関数です。
そのあとは、括弧でくくって、いつも通りに該当する範囲を選択していくだけ。まず最初にやるのはこのグループ1。1群目の数字を選んでください。赤で囲った部分。ここでは、広告Aの日別のクリック数をまず1群目として入れています。次には、青で囲った部分。グループBの日別クリック数ですね。

ただです!ここで初心者を惑わせる、厄介者がついている。この後ろに、2つほど設定を入力しないといけない。そこで「怖いな・・・」と感じてしまうのが人間心理。統計を嫌なものと感じさせる原因です。今日はこの障害も超えておこうと思います。
最初に結論言います!統計学者さん、全国の学者さん、怒らないでください。なんですけども・・この後ろの2つの数字は、ひとまず使う分には、順に2,3と入れればいいです。マジで本当に何もわからないとしても、それで絶対ミスは起こらないです。私としては、とにかく怖くないものだ、便利なものだということをまず経験的に知ってもらいたい。その意味では、あえて、まずは教えません。2,3でいいです。
t検定の詳細設定について
いちおうここはその2,3の説明セクションですが、難しいかな、いいかなと思われた方はここを飛ばして次に行ってください。
まず最初の「2」だと言ったところですが、これは「検定の指定」です。「1.片側検定するんですか?」「2.両側検定するんですか?」というのを聞かれています。片側検定っていうのは、AとBのうち、どちらが数字が大きいかは自明で(仮にA>Bとすると)、BがAを上回ることは絶対にないから、Aのバラツキの下側だけ、Bのバラツキの上側だけ検定すればよいよね、というものです。
論理的に考えて、絶対に数字が逆転する可能性が無い場合のみ、片側検定が使える。ただし、片側検定でOKな場面でも、両側検定のほうが判定が厳しいので、より丁寧な検証になります。なので、こんにち、片側検定はそうそう行われないです。というわけで、改めて強調。「2.両側検定」がデフォです。
次には、検定の種類なんですけど、これも1番2番というのが非常に特殊な条件が成立するときだけ使えるものなので、やっぱりデフォは3なのです。
1番は、データが対のペアになっている状況。同じ人の1年前と現在だとか、全部対になっていて絶対にこのペア同士で比較しなきゃいけないという対のデータのときは1番を選びます。2番目の、等分散のデータ、というのは、グループ1もグループ2も散らばり方が統計学的に同じ構造になっているという、かなり強い仮定が置けるときだけ使える。これはかなり強い仮定で、社会現象においてはそうそう起こるものではありません(自然科学の実験ではあり得ると思います)。上記のような特殊条件のときでも、3.非等分散での検定で、決して間違いではないので、ここまで話を聞いていただいた上で、私としては皆さんは3を選べばよいのではないかなと思います。
結果の解釈
飛ばした方はこちらから。先ほどの数式を入力して、出てきた結果の解釈について!

広告Bと広告Aのこの効果の差、平均値の差、というものについて、0.097という数字が得られた。これは、その差が偶然的に生じる確率が9.7%ということを意味しているわけですね。
このサンプル数(それぞれ2週間分、14件)、このバラツキ、この得られた平均値の差で言えば、同じようにデータを採取していけば、10回に1回くらいは、本当には平均値に差がないにも関わらず、たまたまこういう結果になってしまうこともある、と解釈できるんです。
皆さん、この9.7%という確率を、どう評価するでしょうか。実は古来、学者の世界では5%が基準で、10%はまあ認める、というふうに評価します。

この値、学者はp値(ピーち)と呼びますが、p = 0.05未満ということになってまいりますと、要するに20回やって1回程度しか、偶然的にそうなっちゃう可能性はないということで、ほぼほぼこの2つの数字の平均値に差はあるとみてよいだろうと判断するのです。で、10%ぐらいまでは、まあ2つの数字の間に差があると認めていいんじゃないかな?と判断する。これが、学術界のグローバルスタンダードな数字となっているわけなんです。
で、ビジネスの場合。学術的な理論の検証ということで言えば、p < 0.05とか、p < 0.01を求めていきますが、皆さんも直観的に考えて、「10回のうち9回までは実際に差がある」とすれば、十分な確率だとみてよいのではないかと思われるのではないかと思います。私も、 pが0.1近辺なら、十分な数字です、と日頃お伝えするようにしています。
統計的に有意である、ということ

ちなみに、ちょっと話が横道にそれますが、学術論文の世界では、とにかくこのp値に右往左往しています。どうやったらpの値が0.1を下回るか0.05を下回るのか、ひたすらいろいろ数字をこねくり回して、頑張って0.04目指そう・・・0.05切ろう・・・なんていう事をやっている。もういかなる世界中の学者も天才的な人たちも、ひたすらこの数字に一喜一憂している。果たして本当にこれがアカデミアとして正しい姿なのかという論争があるということは、皆さんにお伝えしておきます。
またその一方でデータサイエンスが非常に普及してきて、多量のデータというものが得られるようになってくると、p<0.01はおろか、p<0.001を目指していくんだという運動もまたあるということも知っておきましょう。自動運転などの世界では、ごめーんこれは間違い判定でした~が p = 0.000000001(10億分の1)だったとしても、世界には10億台の車があるわけで、1日に1台は判定ミスで事故が起こることになります。ものすごい精度を追求している世界もまた、登場してきてるんです。
何にせよ、皆さんがぱっとデータを集めたABテストなんかであれば、このPの値が0.1ぐらいあれば十分と考えてよろしいと思います。
実はここまでの話というのは、学者やデータサイエンティストが言う統計的に有意(ゆうい)とかっていう言葉と密接に関連して、よく学者の先生が「これって統計的に有意とは言い切れないんですよね」とか「統計的な有意差があるのですか」と言うのですが、ここで言っているその統計的有意というのは、先ほど見たPの値が0.1未満だとか0.05未満ということを言っている。統計学的にこの差が偶然的に得られる確率は、5%未満ですか、というのを「それって統計的に有意なんですか」と聞いているわけです。皆さん、学んでしまえば、怖くないですね。これでまた、学者と皆さんとの溝は、1つ埋まったんじゃないかと思います。
ABテストの広告効果検証から、自動運転まで。今日の事業の現場で、様々に活用されることが増えているのがp値です。その基本が学べるという意味でもまずはt検定からですね。エクセルで2列数字をならべて、あとはt.testで判定してくれるので、皆さんも思い立ったらいますぐエクセル開いて、ものの2‐3分でできるはずです。ぜひ、身に着けてしまってください!!
著者・監修者
-

1982年生。経営学者/やさしいビジネススクール学長/YouTuber/経済学博士/関東学院大学 特任教授/法政大学イノベーション・マネジメント研究センター 客員研究員
詳しい講師紹介はこちら website twitter facebook youtube tiktok researchmap J-Global Amazon
専門は、経営戦略論・イノベーション・マネジメント、国際経営。
「アカデミーの力を社会に」をライフワークに据え、日本のビジネス力の底上げと、学術知による社会課題の解決を目指す。
「やさしいビジネススクール」を中心に、YouTube・研修・講演・コンサル・著作等で経営知識の普及に尽力中。


コメント