ウイルス陽性反応、あなたが本当に感染している確率は?(ベイズの公式)【やさしい統計学11】

ビジネスパーソンのためのやさしい統計学「第11回目」
※YouTubeにて各シリーズ連載中
今日はめちゃくちゃ大切な会なので最後まで必見です。
どういう感じなのかというと、あなたが自分は感染してないよな?と思ってPCR検査を街中で受けたとします。
そして、陽性という結果が得られたとして、その時、「あなたが本当に感染している確率はどれぐらいなのか」ということを説明していきます。ここで本当に皆さんは驚きの結果を目の当たりにすることになりますので、最後まで注目していってください。
また、この話の流れの中で皆さんは、ビジネスでも使えるベイズの公式という非常に使いやすい理論ツールを学習してもらいますので、それも楽しみにしてもらえたらと思います。
さて。今では、陰性証明ということを獲得するために、PCR検査というのが街中どこでも受けられるようになっています。で、陰性証明は出せるわけなんですけれども、逆にウイルス検査で陽性になってしまったとき、これが偽陽性である確率というのはどれくらいなのか、私は、皆さんに絶対に知っておいていただきたいのです。
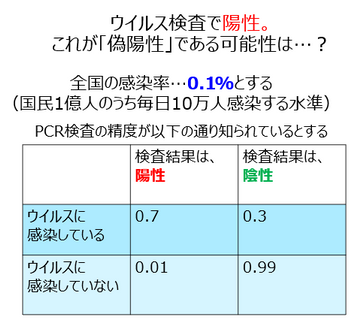
ウイルス検査で陽性、「疑陽性」である可能性は?
PCR検査というのは、過去のサンプルの蓄積で、おおむねこういう結果になるということはわかっています(下図)。あなたがウイルスに感染していたとして検査結果が陽性になるのは70%。なんと、見過ごされてしまう確率も30%存在しているわけなんですけれども、一方、ウイルスに感染していない時は、どのようになるかというと、そこで偽陽性になってしまう確率というのは、わずかに1%。99%まではあなたは陰性ですよ、ということを証明してくれるんだということになるわけなんです。
ベイズの公式
この数字だけ見ると、あなたが陽性だという結果になったならば、ほとんど確実に感染してるじゃないか、と思ってしまうじゃないですか。
しかしこれ実は、数字のマジックというやつなんです。
今から皆さんと、ちょっと数式を展開していきますが、難しくないのでご安心ください。
それを追いかけていきますと、あなたが本当に陽性である確率というのがここから見えてくる。
仮に、全国での1日の感染者数が0.1%だったとしましょう。1.2億人の人口の国で、12万人が0.1%にあたります。1日12万人。だいぶ、大きい数字ですね。0.1%の感染率といっても、凄く大きい数字だとわかります。日本では、2021年の2月3月が、大体これぐらいでした。
先ほども言いましたが、今回使うのはベイズの公式という数式・理論なんですけれど、これというのは、条件Aのもとで、Bが起こる確率を、条件Bのもとで、Aが起こる確率に置き換えることができる公式なんです。(ベイズの公式の基本解説はこちら。)
今回の例で言えば、私たちはいま、「ウイルスに感染しているかどうか(A)という条件のもとで、PCR検査の結果が陽性になるかどうか(B)」という確率を手にしているわけです。これを、ひっくり返せる。すなわち、「PCR検査の結果が陽性であるときに(B)ウイルスに真に感染しているかどうか(A)の確率」に、置き換えられるのがベイズの公式です。
これを使うと偽陽性の確率が求まってくるわけで、実はこのベイズの公式というのは、この疫学、感染症の研究分野でめちゃくちゃ重要な理論になってるわけなんです。
今日はこのベイズの公式を、直感的に理解してもたいます。
順を追っていただけば、ベイズの公式を理解するとともに、検査結果が陽性であったときに、偽陽性である確率も見えてまいります。
さて、現在は、横(行)方向の条件に対して確率が求まっているという状態になっているわけです(下図赤枠)。
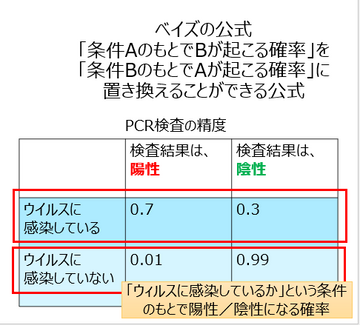
これを列方向の確立に置き換えられる、というのがベイズの公式なんです。
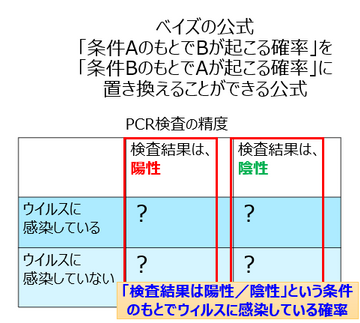
先ほど条件のAもとで、Bがというのが・・・ちょっと分かりにくかったかもしれませんが、こうやって表現すると分かりやすくなると思いませんか?この縦の方で確率を計算し直したらどうなるのか、というのがベイズの公式なんです。
ベイズの公式を実際にどうやって計算するのか
ベイズの公式、実際にどうやって計算していくのか、というと結局この全体に占める4象限の割合というのを求めていくということをやっていくんですね。全国の人々に無作為にPCR検査をしたら、全ての人は、必ずこの4象限のうちのどこかに当てはまる。なので、PCR検査を10000人に実行したとしたら、10000人の人がこのどこかに散らばるわけで、その割合を求めてみましょう!というのがベイズの公式の考え方です。全体に占める割合はどうなるのか、というのを計算してみる。
ここでどの数字が役に立つかというと、全国の感染率が0.1%という数字が役に立ってくるわけですね。そうすると、このご覧の通り、この0.1%という数字は、この行上の方の行ウイルスに感染しているは全体の0.1%という情報が使えまして、下側ウイルスに感染した人は全体の99.9%ということで、まず上と下このように分類ができるわけじゃないですか。上になる人はわずかに10人、残り9990人は下になるわけですね。
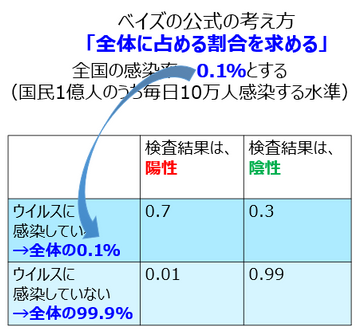
とすると、この0.1%の人、10人のうち、更にそのうちの7割の人というのが、検査結果で陽性になる。残り3割の人は、検査結果で陰性になる。ということで、この0.1%と掛け算をしていきますと、それぞれのボックスに収まる人が何%ぐらいの人以内なのか、ということが求まってくるわけです。
ウイルスに感染していて、検査が要請になるのは、10000人いて、7人です。
残念ながら3人が偽陰性で見落とされてもしまうのですが、まずは「PCR検査を無作為に実施したら、10000人いて7人しか検出されない」ことを頭に入れておきましょう。
下も同じですね。ウイルスに感染していない全体の99.9%の人のうちのわずかに1%0.01の割合の人だけが陽性になって、それ以外は陰性になるわけで、このように見てみますと、皆さん、一目瞭然!大半の人が右下ウイルスに感染しておらず、検査結果も陰性0.99×0.999ということで、大半の人がここに収まってくるということが分かるかと思います。10000人を配分すると、ウイルスに感染していないのにPCR検査が陽性になる人は、99人もいることになる。無作為実施すれば、全体の1%くらいの人は、偽陽性になるんです。なお、ウイルスに感染しておらず、検査結果が陰性の人は、9890人です。
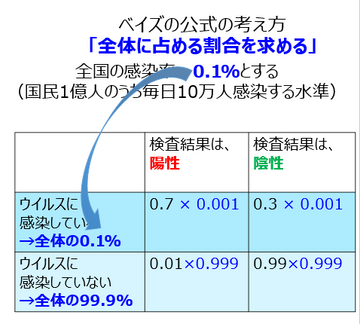
計算してみた結果がこんな感じです。
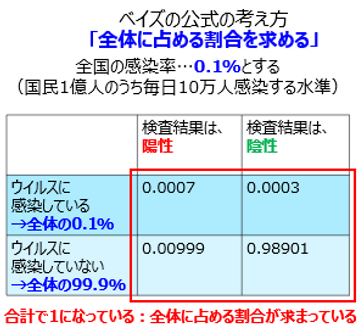
無作為にPCR検査を国民すべてに実施すれば、この4象限にこのような確率で散らばるということが分かるわけです。合計で1になっているということも、皆さん念のため確認してください。
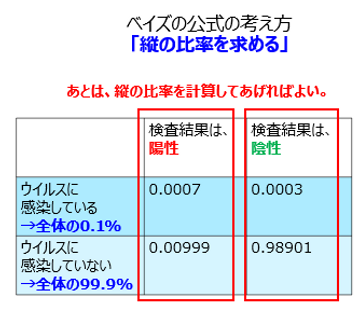
もう、この表が得られてしまえば、皆さんは何も難しいことはないですね。検査結果が陽性になったとき、ウイルスに感染している確率は、どれくらいでしょう。縦(列)方向に見ていけばよいのですね。数字を揃えると、以下のようになります。
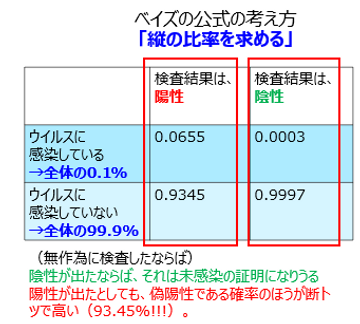
ということで、これがベイズの公式というものです。これを使いますと、何がまとまるのか・・・そう、偽陽性の確率が求まってしまう、でしたね。この検査結果が陽性であったとして、あなたが真にウイルスに感染している確率は0.0655。わずかに6.5%しか真にウイルスに感染している人なんていないわけなんです。
残り93.45%の人は検査結果が陽性であったとしても、ウイルスに感染していない。偽陽性が、なんと93.45%を占めてしまうわけなんです。
陰性の証明
一方で、この右側見るとわかりやすいです、陰性の方は証明できるわけです。
陰性結果が出たとして、あなたがウイルスに実は感染しているんです。という確率が0.0003ということで、陰性はほぼ証明できるわけですね。だから、陰性証明なんです。陰性が出たらほとんど確実にウイルスに感染していないと言えます。
しかし、陽性時は証明できないのです。陽性を得たとして、実は大半の人、93%までもが偽陽性なんです。そんなわけで、まずはこのPCR検査の結果に対しての解釈という事をちょっとまとめておきましょうか。
ご覧の通り、疫学というのは、このベイズの公式というものを活用していまして、実験の結果で得られたこの検査というのは、どれくらいの精度で分析できるんだろうか、そのデータを元に今の入れ替えをして、陽性だとか陰性がどれくらいの確率で証明できるのか、これをチェックした上で国民に施していくのが各種の病気に対する検査なわけです。
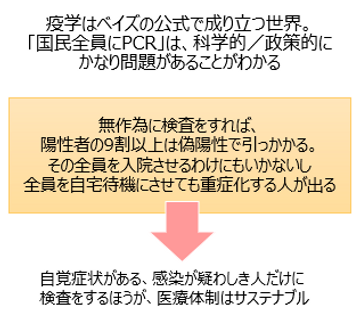
一般論としてその疾病にかかっている人という割合が遥かに小さいために、無作為に検査をしたとすれば陽性反応が出たとして、コロナでなくても何でもそうなんですが、9割以上は偽陽性です。なので、症状が無い人に検査をするのは、ほとんど意味がない。10000人に検査をして、わずかに7人しか、検出できない(99人の偽陽性を出しながら)。
だから、自覚症状がある人に絞って検査をし、さらに2度3度と別種の検査をして、結果をチェックしていくことなんです。陽性が出たとして、それはあなたがその疾病にかかっている、ということの証明にはならないわけなんです。
だとするとです。
国内ではこんな論調があります。
国民全員にPCR検査をやって私達は安心させるべきなんじゃないのか、というような論調。これが、科学的に間違いだということを、皆さんお気づきいただけたのではないかと思います。陽性者の9割以上は偽陽性であるとするならば、その全員を病院に入院させたところで問題ですよね。病院に入院している大半は感染していないわけなんですから。だとすると、その人達を入院させてしまったら、医療体制が逼迫してしまいます。
かといって、偽陽性が9割なんだから全員自宅待機にさせましょう。誰が感染しても分からないからね。ということで陽性が出ていながらもみんなを自宅待機させてしまうと、中には本当に感染している人がいて、そういう人が重症化してしまう、取り返しのつかないことになってしまうかもしれないです。
だから、無作為に国民全員にPCR検査をするのはやるべきではない。自分は感染したのではないか、というような濃厚接触の疑いがある人、感染可能性の高い場所から戻ってきた人、自覚症状がある人だけ検査をしていく、というのが妥当な方法だと考えられているのです。
という訳で、皆さんお分かりいただけたのではないかと思いますけれども、めちゃくちゃ大切な考え方です。ベイズの公式。そして、この考え方というのは何も感染症疫学だけじゃなくて、ビジネスの現場でも様々に応用ができます。
ベイズの公式が数字の見方をクリアにしてくれる
このベイズの公式の考え方、条件AのもとでBが起こる確率。条件BのもとでAが起こる確率。行方向に分散していた確率の列方向に書き直せる手法。これというのは、あなたの数字の見方をもう少しクリアにしてくれる。ということは分かりましたね。
ビジネスの現場でも、考え方としても大切です。一見してこれは、効果がありそうだと思われる手法であったとしても、ちょっと行列で計算し直してみましょうか、とチェックすると、あれ、意外と効果無かったんじゃないのかな、ということもある。もちろん、その逆もある。効果が無いかなと思っていた手法が、行列を書き直してみたら「結構効果あるやんけ」となる可能性もあるわけなので、このベイズの公式の考え方を是非、あなたのお仕事の中でも、生きる手法として身につけてもらえたら、学んでもらえたらと願っております。
著者・監修者
-

1982年生。経営学者/やさしいビジネススクール学長/YouTuber/経済学博士/関東学院大学 特任教授/法政大学イノベーション・マネジメント研究センター 客員研究員
詳しい講師紹介はこちら website twitter facebook youtube tiktok researchmap J-Global Amazon
専門は、経営戦略論・イノベーション・マネジメント、国際経営。
「アカデミーの力を社会に」をライフワークに据え、日本のビジネス力の底上げと、学術知による社会課題の解決を目指す。
「やさしいビジネススクール」を中心に、YouTube・研修・講演・コンサル・著作等で経営知識の普及に尽力中。

コメント