ビジネスパーソンのための優しい統計「第5回目」
※YouTubeにて各シリーズ連載中
今回は、実際にエクセルを使って、度数分布図を書く技術を身に付けてみましょう。
エクセルで度数分布グラフを書く
今回は、「データの散らばりがどういうふうになっているか」を分析していくのですが、今回も前回(エクセルで平均値・中央値・最頻値を出す!)で使ったものと同じデータを使っていきます。皆さんもダウンロードできますので、データ分析の練習に使ってみてもらえたら嬉しいです!
とはいえ、今回から見ている方もいると思うので、どういうデータか説明すると、50人の人に、商品AからFまで6種類の商品について、「全くいらない」から「非常に欲しい」までの5段階で評価をしていただいたマーケティング調査のデータになっています(架空のデータです)。この5段階評価から、6種の製品の「どれが一番人気か」を分析し、これからの商品展開を考える。
前回は、このデータの平均値・中央値・最頻値を求めて、どの商品が人気かを調べ、商品Dが一番人気だろうと検討をつけていました。
ただし、平均などを見ただけでは、データの散らばり方がわかりません。本当に商品Dで決めてしまってよいのか、賢明に判断するなら、回答がどう散らばっているかも見るべきです。
データの散らばりを見る
そこで今回やるのが、散らばりを見る技法です。って、何をするのがいいのか。
散らばりを表す統計の値としては、標準偏差というものがあります。
標準偏差という値は、平均値からどれくらい散らばっているのか、標準偏差±1の間に、およそデータの6割ぐらいが含まれてくるということで、標準偏差を見ると、なんとなく散らばりの全体像が見えてくるわけです。でも、結局、標準偏差という値を使っても、本当の回答の散らばりはわからない。私達人間が見て、本当に解釈できるものこそが望ましい。
エクセルでどう修正するのか
では、実際に標準偏差を見てみたいと思います。ここからまた、エクセルの時間です。
ここで標準偏差を分析するときの関数というのは、
=STDEV(セルの範囲)
このように指定します。Standard Deviation(標準偏差)からとって、StDev。ちなみに、エクセルの関数は大文字小文字を区別しないので、どう書いても大丈夫です。私はいつも小文字で書きます。シフトキー押すのが面倒ですからね。エクセルは自動的に全部大文字に修正してくれるので、わざわざ大文字で書く必要はありません。
ただし、実は新しいExcelでは、これをさらに、「STDEV.p」「STDEV.s」いう形に統計学の理論に基づいて細かく分けて分析していくかたちになっています。まあ、昔から互換性がある、「STDEV」でいいんじゃないかと、私は思います笑。
で、あとは図の関数入力欄のとおり、範囲を指定すれば、5段階評価がどうばらついているのかが計算されます(図中B5のセル)。
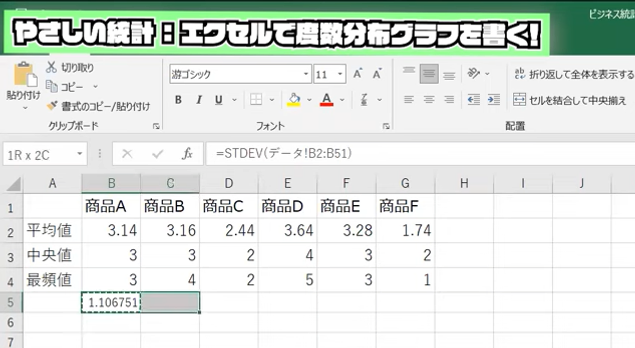
ご覧の通り、1.106…という数字が出てまいりました。これは商品Aの回答の標準偏差です。プラスマイナス1.106の範囲内に、およそ6割の回答が入っている。平均が3.14ですから、2か3か4を選択しているのが、6割の回答だということになります 。
あとは、比較分析するためには、これを商品B~Fにも実行すればよい。
「Ctrl+C」でコピーして、
Shiftキーを押しながら横にピーっと引っ張れば横のせるにドラッグすることができ、
「Ctrl+V」で貼り付けます。
これ、身に着けて覚えてしまいましょう。めちゃくちゃ時短です。
ここまで、覚えてしまえば、商品Aに入力するところも含めて、1分かかりません。
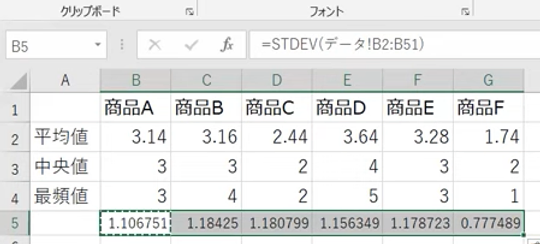
上図がコピーペースト完了後です。
…ちょっと、見づらいですよね。桁数が多すぎるんだ。
ここで、どうするのか。もうひとつ、ちょっとした技を知っておきましょう。
エクセルで桁数を減らして表示するボタンというのは、標準で搭載されています。
メニュー欄に、「桁数をいくつ減らします?」「いくつ増やしますか?」があるんですね。
↓これ!!↓
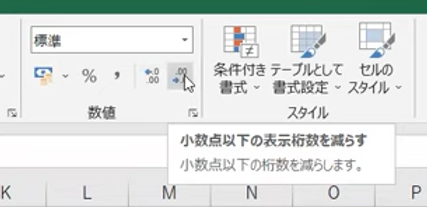
左側が小数点以下の表示桁数を増やす、右側が小数点以下の表示桁数を減らす!
実際にやってみた結果がこちらです。めっちゃ見やすくなりましたね。
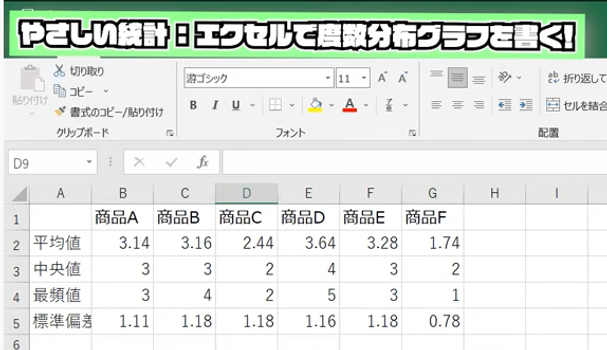
でも、どうでしょう。
この数字見て皆さん、それぞれの散らばりがどうなっているか、わかりますでしょうか。
そうなんです。
統計学的には重要だし、高度な解析を行うときには必須の概念ではあるのですが、標準偏差では、散らばりの実態はわからないのです。
たとえば、商品A、B、E。平均値、中央値、最頻値、そして標準偏差とみても、どれが人気あるのかは、ちょっとわかんないですよね。
標準偏差というのはそもそもそういうデータなのです。
では、どうするか。
もっと素朴な方法こそが最強。
棒グラフです。
棒グラフの書き方
棒グラフ、まじ最強。
ただし、エクセルで出力するには、実はこれまでよりもひと手間、技術がいります。回答1~5までが、何件あるのかを、集計しなければいけないからです。
回答1が何件あるのか?それを計算する関数!
=COUNTIF(探す範囲, 探す数値)
めちゃくちゃよく使う関数なので、覚えておきましょう。カウントイフ、が読み方ですね。今回だと、こんな感じ。
=COUNTIF(データ!B2:B51, 1)
これで、「データ」のシート内のB2~B51の範囲内で、1が何件あるかをカウントしてくれる。
で、先ほど同様、これを横にコピーしていけば、商品A~Fについて、回答1の件数が簡単に求まります(下図6行目)。
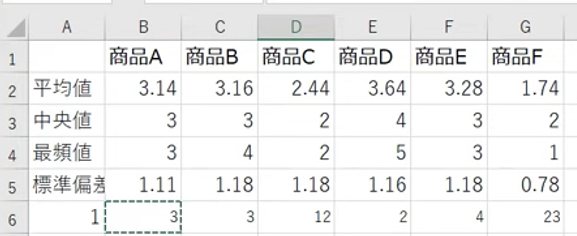
ただ、これを縦にコピーしていくと、位置がずれてしまうのが問題ですね。ですから、絶対位置指定の$を使ってやる。
=COUNTIF(データ!B$2:B$51, 1)
ブルーで書いたところ。このドルマークは、その右側の値をコピーしても動かしませんよという命令です。
1つ下にコピーすると、$マークを打たないとB3:B52に、1個ずれてしまう。
でも、$を付けておくと、B$2:B$51のまま、変わらないんですね。
さらにもう1つ、楽にしましょう。COUNTIFの数式の、一番最後のところ。「1」を指定していますが、これが自動的に「2」「3」と変わっていったらいいですよね。そこで、ここを指定してやる。
A列に、12345を書いておくわけです。そして、ここを参照させる。
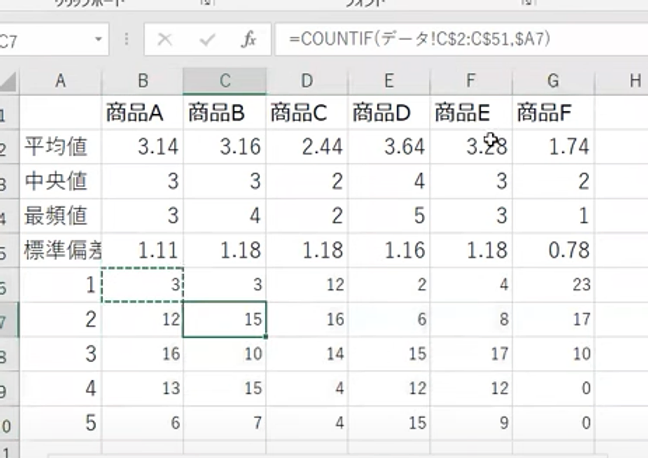
=CONTIF(データ!B$2:B$51,$A6)
今度はAの前に$を付けておき、Aが動かないように固定する。こんがらがる人もいると思うので、ここで、よくよく私が何をしているのか、自分なりに理解して、なるべくなら自分で操作してみるといいかもしれませんね!
ここまでできれば、もうしめたものですね。これをコピーペーストしてやれば、商品A~Fについて、1から5までの回答数が求まります。
実際にグラフで出してみる
実際にこれをグラフで出してみます。
グラフで出すのは、エクセルさんがあらゆる統計ソフトの中で圧倒的に強いです。グラフで出したい範囲を指定して、「挿入」ボタンを押せば、グラフの初期デフォルト設定の中から直観的に選ぶことができます。(挿入ボタンは下図の左上のほうに見つかるはずです。その後、赤枠のところでおすすめグラフから選択すると、即座にグラフが表示されるはずです。)
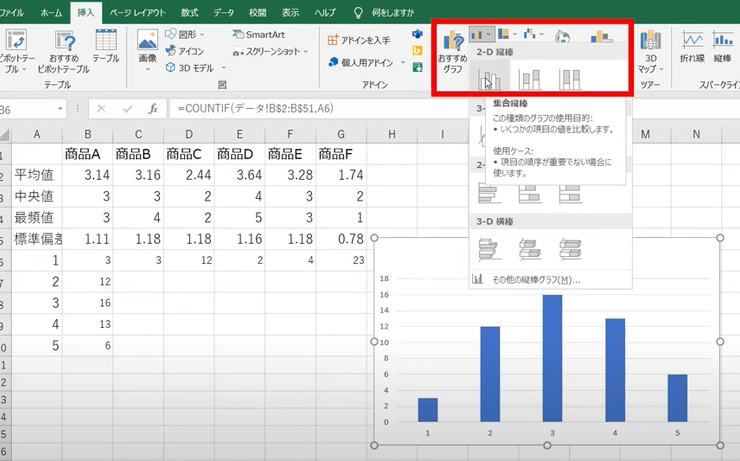
なんら苦労することなく、自動でグラフが出てしまいました。めちゃくちゃ、簡単ですね。
これ見たらもう皆さん納得いただけますよね。ここまでの平均値、中央値、最頻値、標準偏差も確かに大切ですけど、それ以上に私達に雄弁に語ってくるのはグラフです。この商品Aに関する回答の棒グラフをみれば、3が最多の回答であることはすぐわかる。
あとは同様に商品Fまで全部出してやればいいだけ!
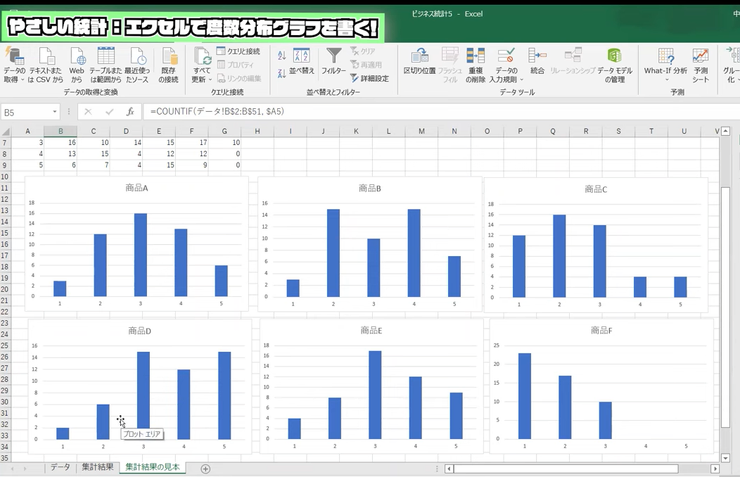
ここまで、皆さんが実際にデータを操作してたどり着けたなら、結構レベルアップになったなと感じてもらえているのではないかと思います。
そして、この棒グラフからは、平均値だとか標準偏差では見えなかったものが見えていることもわかるはずです。例えば商品AとBを比較してみましょう。同じような平均値と標準偏差だったのですが、AとBではこんなに回答の傾向が違う。最頻値をみるとAが3、Bが4だったので、Bのほうが売れているのだろうと思われたのですが、Bは「好き嫌いが分かれる商品」だったのです。何度も言いますが、グラフにしてみること、とても重要ですね。
ご覧の通り、グラフで書いて、ようやくどの商品に対して、人々がどういう評価を下したのか、確信ができる。かならずグラフで見てみる。これをどうか忘れないでほしいのです。
そんなわけで、今回はデータの散らばりを見つつ、色々tエクセルの操作方法もお伝えしてきました。皆さんが今後もこうして、一緒に新しい知識を手に入れていってもらえたらと願わずには、いられません。
著者・監修者
-

1982年生。経営学者/やさしいビジネススクール学長/YouTuber/経済学博士/関東学院大学 特任教授/法政大学イノベーション・マネジメント研究センター 客員研究員
詳しい講師紹介はこちら website twitter facebook youtube tiktok researchmap J-Global Amazon
専門は、経営戦略論・イノベーション・マネジメント、国際経営。
「アカデミーの力を社会に」をライフワークに据え、日本のビジネス力の底上げと、学術知による社会課題の解決を目指す。
「やさしいビジネススクール」を中心に、YouTube・研修・講演・コンサル・著作等で経営知識の普及に尽力中。

コメント