更新日:7月10日
チャート図を統計的に証明できる!構造方程式モデリング!【やさしい統計学17】

ビジネスパーソンのためのやさしい統計学「17」
※YouTubeにて各シリーズ連載中
今日は最初にお伝えしておきますと、だいたいの概要を掴んでいただければ、それでOKです。
必死に覚えなきゃいけない!自分で使えるようにしなきゃいけない!そういうのは一切ありません。今から、私がお見せする手法というものを、なんか面白そう。と思っていただければそれでOKです。あなたが一般のビジネスパーソンとして、構造方程式モデリングを実施することは、ほとんどありません。あなたに求められるのは、その結果を正しく解釈し、ビジネスに応用できることです。
構造方式モデリング:SEM
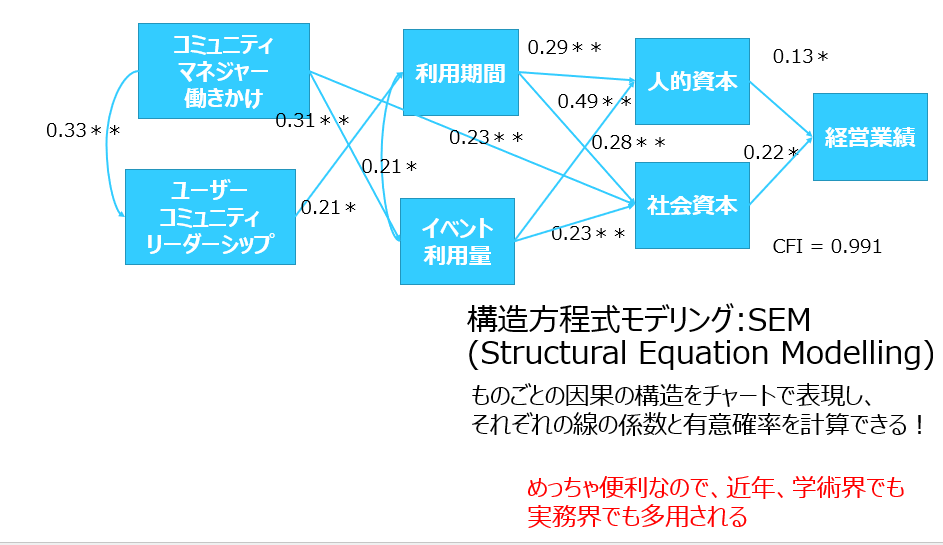
構造方程式モデリングというのは、こんな感じの長いチャート図なんですね。
こういうチャート図って、遊びでも仕事でも、書くことってあるんじゃないかと思うんです。で、近年は、このチャート図を統計的に実証することができる時代になっている、という話なんです。
構造方程式モデリングとは、Structural equation modeling、略して、SEM(セム)なんていいます。最近、非常に注目されるようになっているのですが、その理由は至ってシンプル。だって、チャート図が統計的に証明できるんですよ。学者がいろんな事象を証明するときにも、このSEMが非常に便利でして、今日では論文でも非常に多用されるようになっています。
経営学、経済学の論文でも非常に多用されていますし、上図をパッと見ておわかりいただけますように、ビジネスにも、めちゃくちゃ使い勝手がいいわけなんです。なので、もう学者として全力でおすすめです。何か統計解析やってみよう!と思ったら、この構造方程式モデリングです。重回帰分析などよりも、遥かに直観的でわかりやすい。
しかも、この構造方程式モデリング、何が良いかって、結果が出やすいんです。回帰分析だとかは、なかなか結果が思ったように出ないことが多い。そんな中、この構想方程式モデリングは、人間的な直感に近い感じでモデルを書いては、簡単に結果が得られるとあって、大人気なのです。
ということで、何度も言いますが、
✓学者の論文でも非常によく出てくる
✓データサイエンティストがやる研究もこの手法が使われます
✓そしてビジネスの現場でもとても使い勝手がいいわけなんです。
ただ、前回説明したロジスティック回帰みたいな、厳密にAかBかを判定するっていうのには、向かない。膨大なデータで機械学習を行って、99.999%の精度を追求する、そういう手法ではないのです。回帰分析は、厳密さを追求するもの。一方で、SEMは、人間が直観的に理解しやすいもの、と思ってください。
読み方も何の難しさもない。マイナスに大きければ大きいほどマイナスの効果が強く、プラスに数値が大きければプラスの効果が強い。それだけです。かつ、その横には*マークついていますが、これも、本シリーズを見てきた人ならもう怖くないですね。統計的に有意である、ということ。*マークが1個付いていれば、結果が単なる偶然である確率が5%未満、非常に信頼性の高い結果だということになる。*マークが二つ付いてれば、偶然の可能性は1%未満、三つ付いていれば0.1%未満ということで、この星マークがついているやつを信頼していけばいいわけなんです。
それから、もう1個注目する点としてはですね、ここにCFI=0.91という数字がありますが、これって何なのかと言いますと、この全体の事象のうちの当てはまりが何%ぐらいかな?ということ。91%ということは、データが示唆する因果関係のうち、ほぼ9割までが記述できていることになる。SEM、実態記述の手段として、すばらしい描写力です。
結果を解釈してみる

今、見て頂いているのは、私が行った研究の実際の結果なんです。民間のコワーキングスペース運営会社さんと一緒に、そのコワーキングスペースの中で、ハイパフォーマンスな人は、どういう動き方をしているのかな?というようなことを、調べた研究。
何が見えてきているかといえば、まずコミュニティマネージャーが場に積極的に働きかけていくと、イベントの利用頻度が高まっていく。また、コミュニティマネージャーからの働きかけは、社会資本、すなわち人々のその現場の繋がり合いも高まっていく。
また、コミュニティリーダーシップも影響している。調査対象者が、自分のいるコワーキングスペース内でリーダーシップを発揮して、その場を良くしようとされていらっしゃると、利用期間に効いてくる。それは社会資本にも繋がってくるし、人的資本、すなわち自分の技能形成にも繋がってくる。
イベント利用率の高まりもまた人的資本、社会資本を高める。で、それが結局、自分の仕事の業績アップに効いてくるわけです。ということで、どうですかね?とっても大切なことが証明できていると思うんです。
コワーキングスペース運営者としましては、コミュニティマネージャーの働きかけや、ユーザーがリーダーシップを発揮してもらえるような場にしていくこと、またイベントをたくさん開催していくこと、これらを通じてその中にいる人たちのパフォーマンスを高めることができるということが証明された。一方、コワーキングスペース利用者さんにとっては、やっぱりこのイベントに参加していったりとか、長く利用していく中で人的資本社会資本を高めていったりすることで、業績が上がっていく、そんなことが証明できたわけです。
どうです?めちゃくちゃ便利で、めちゃくちゃいい手法だと思いませんか?
構造方程式モデリングは何に秀でているのか
構造方程式モデリング、ちょっとだけ何がスゴイのかを説明しておきましょう。
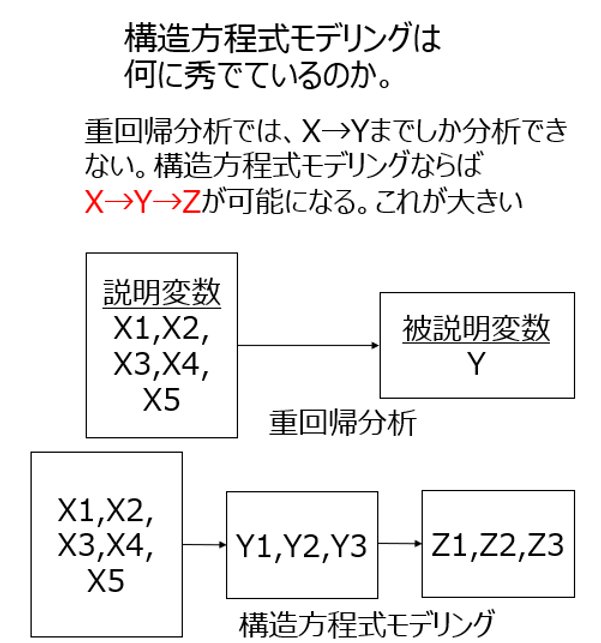
SEMが何に秀でているのかなんですけれども、これまで私達学者が使ってきた回帰分析というモデルでは、XとYという、ある要因がある結果をもたらしている、このXとYの関係までしか分析できなかったんですね。ところが、構造方程式モデリングなら先ほど見ていただきましたように、XYZ、さらにその先という形で、長い因果のモデルを検証できるようになるわけなんです。
今まで、それを検証できる統計分析手法がなかった中で、SEMは大きな手法的前進だと言えるわけなんです。
ダマされないand誤解しないための読解ポイント

めちゃくちゃ便利な手法なんですが、実際のところ、分析自体はごく初歩的なことをやっています。エクセルなんかでも出せる相関関係を可視化しているに過ぎないんです。
ですから、例によって統計ソフトの中にぶち込むと、パパパッ!と結果が出てくる。とそういうレベルのものなので、例えば、クラウドソーシングしていただいて、データサイエンティストさんと一緒になって、「ちょっとうちの会社についてこういうことを調べてみたいんだけど」とか「マーケティングについてこういうことを調べてみたいんだけど」など、やろうと思えばすぐに、かつ、安価に、分析できてしまいます。
そういう性質のものであるがゆえに、結果を誤解しないようにすることが、ここで大切になります。
第1には、その因果の順序、すなわち矢印の向きは、論理的に考えて正しいかどうかをよく吟味すること。この矢印の向きって、人間が指定してやってるんですよ。機械が自動判定しているんじゃないんです。人が決めてる。
「こういう因果関係なっているんじゃないのか?」というのを、機械が自動的に出してくれているわけではない。人間が、「こういうふうになっているんじゃないのか?」っていう絵を描いて、それを機械に検証させている。人間のロジックの制約を受けているわけです。
だから、逆の因果関係になっていたりすることもありうる。このチャート図が正しいかどうかは、機械の精度じゃなくて、もっぱら分析者の思考に依存するんです。
なので、うっかりすると、よく考えたらおかしい因果関係になっていたりします。この点、読み間違えないようにしましょう。
それから第2。*マークはやっぱりめちゃくちゃ大切です。このSEMというもの、先にお伝えしたように、良好な結果が出やすい。良好とはつまり、*マークがつきやすいということ。パパッとどんな分析をしても、大体それっぽい結果を返してくるのです。
だからこそ、*マークの有無には、こだわりたい。これだけ結果が出やすい手法で*マークがついていない関係というのは、その矢印はごくごく信用ならないと考えた方が良いです。
それから第3には先ほど、チラッとお話ししたCFIですよね。先ほど0.91と見せましたけれども、実はこの構造方程式モデリングのこのCFIは軽く0.9を超えてくるんです。逆にいえば、SEMにおいて、CFIが0.8を割り込んだら、かなり疑わしいモデルだと見てよろしいのではないかと思います。
何にせよ、ちょっと細かい話をしましたが、原点に立ち返れば、難しく考えずに、ぜひあなたの現場で使ってみていただきたい。
最初に言いましたように、データ分析というのは「あんな手法を使えたらおもしろそう」「ちょっと使ってみようかな?」という感覚を持ってもらえるのが最良。抵抗を感じる前にスッとやってみてしまう。これです。で、やろうと思ったらクラウドソーシングでもいいし、身近にいる人でできそうな人に聴いてみるのでもいい。私(中川)だって力になれます。
ぜひ、怖がらずに、へえ、こういう世界があるんだと、知っていてくださったら嬉しいです。
著者・監修者
-

1982年生。経営学者/やさしいビジネススクール学長/YouTuber/経済学博士/関東学院大学 特任教授/法政大学イノベーション・マネジメント研究センター 客員研究員
詳しい講師紹介はこちら website twitter facebook youtube tiktok researchmap J-Global Amazon
専門は、経営戦略論・イノベーション・マネジメント、国際経営。
「アカデミーの力を社会に」をライフワークに据え、日本のビジネス力の底上げと、学術知による社会課題の解決を目指す。
「やさしいビジネススクール」を中心に、YouTube・研修・講演・コンサル・著作等で経営知識の普及に尽力中。


コメント