更新日:6月5日
ビジネスパーソンのための優しい統計「第8回目」

※YouTubeにて各シリーズ連載中
相関係数というのはどういう状況で使うのか。例えば、私のような学者だとかデータアナリストが結構使うんです。ぱっと二つの数字の間の関係を数量的にとらまえるときに使うんです。
散布図は最強だけど大変
でも、過去にはいくつかの講義で言ってきたんですけれども、二つの数字の間の関係を分析するときというのは、散布図が最強です。散布図を見てみないことには、現実の2つの数字の関係はわからない。だから、散布図を見ましょうね、これが原理原則なんです。
相関係数は簡便
なんですけれども、例えば売上高みたいな値をYとしたとき、いろんなXの候補がありうるわけです。広告投資だとか製品のラインナップだとかいろんなものがバーっと存在している中で、数十もそのXの候補がある中で言うと、数10回散布図をつくるなんていうのは、確かに面倒くさいですね。
社内外のデータアナリストにお願いするにしても、全部それを出力して、分析までしていただくっていうのは、かなり現実的ではないわけです。
そんなとき、関係ありそうなものをざっとピックアップするために役に立つのが、相関係数という値です。
数式計算でぱっとエクセルが一瞬で求めてくれて、その数字を見ていけば、これとこれとこれが関係ありそうだな、というのを目星をつけられる。その意味で、相関係数は本当に有効なものなんです。
活用してみよう
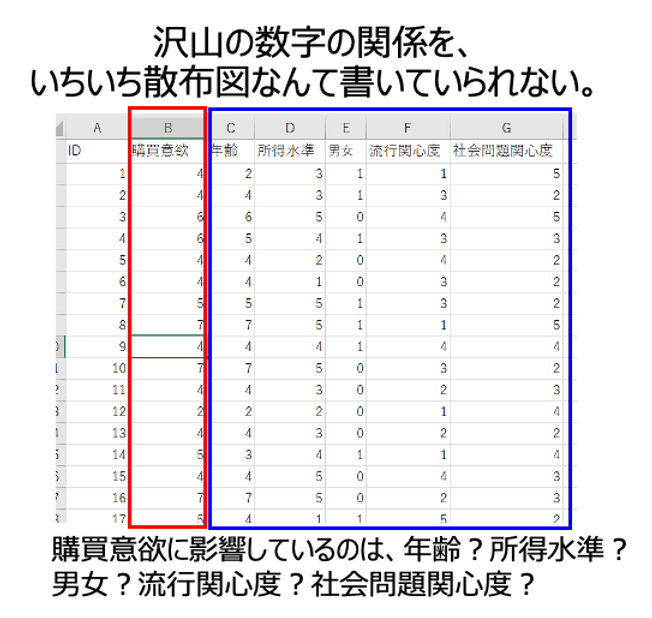
例えば購買意欲というものに対して、年齢、所得水準、男女流行監視の社会問題関心度、こんなようないくつかのものがあって、果たしてどれが関係しているのか。
いちいち全部散布図を書いていくっていうのはちょっと現実的じゃないわけですね。
またさらにもう1点追加しておきますと、アンケートで5段階評価や7段階評価で回答すると、散布図を書いて、例えばxもyも3でしたっていうときには、この(3, 3)の座標のところに、多数のサンプルが積み重なってしまいます。
この積み重なりを表現しようと思ったら、3次元描画になってしまうので、これまたひと手間だし、ちゃんと分析するのがやっぱり難しくなってしまう、そんなようなときに生きるのが、相関係数です。
相関係数”R”
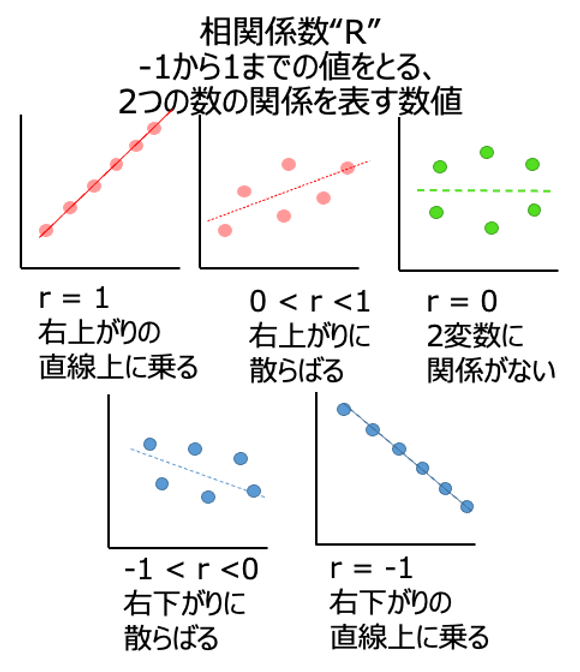
相関係数というのは、この統計学の世界の中でRと表現します。小文字でrで書くことも多いんですけれども、この相関係数Rというのはマイナス1からプラスの1までの間をとります。
R=1というのは完全正比例状態ですね。
右上がりの直線上に点が並んでいる状態、このXとYの間にこの直線になるような、散らばりも全くなく完全直線上の関係があるという状態がR=1の状態です。
そして、Rがプラスの正の値をとってる間というのは、右肩上がりの関係で、当然このRの値が高ければ高いほど傾きが明確になります。このRの値が0に近づいていくほど、関係が不明瞭になる。
そして、Rがゼロというのは、無相関という言い方をします。
二つの数字の間にまったく関係が見て取れないんですよ、というような状態が、R=0ということです。
そして、Rがマイナスの方に入ってくると、今度はは右下がりになってきます。R=-1というのは完全直線上の右下がりの関係になるんだということを意味しています。
この感覚さえ理解しておけばOKです。2つの数字の間に、どれくらいのプラスorマイナスの関係があるか、というような数字だと思っていただければ、十分皆さんが分析に使っていただけます。
エクセルで簡単に相関係数を求める
そして、これをエクセルでやるのもめちゃくちゃ簡単なんです。これは知ってると知らないと結構わかれてくるポイントです。知っていればすぐに皆さんの武器になりますから、ぜひ皆さんもエクセルで再現してみてください。

エクセルで使う関数は、correl関数です。
correlation(co=共通)(relation=関係)で、「共通の関係→相関」となってcorrel関数と表ます。
エクセルでcorrelというふうにセルにイコールを付けて入力していただいて、1個目の数列と2個目の数列を並べて選択していただければ、ぱっと簡単に相関係数を求めることができます。
実際に使ってみましょう
この処理も平均値だとか分散を求めるのとさして変わらないので、ここまで皆さんに学んできていただいた方、手法を使っていただければ、すぐにこのcorrel関数というのも使えるようになります。
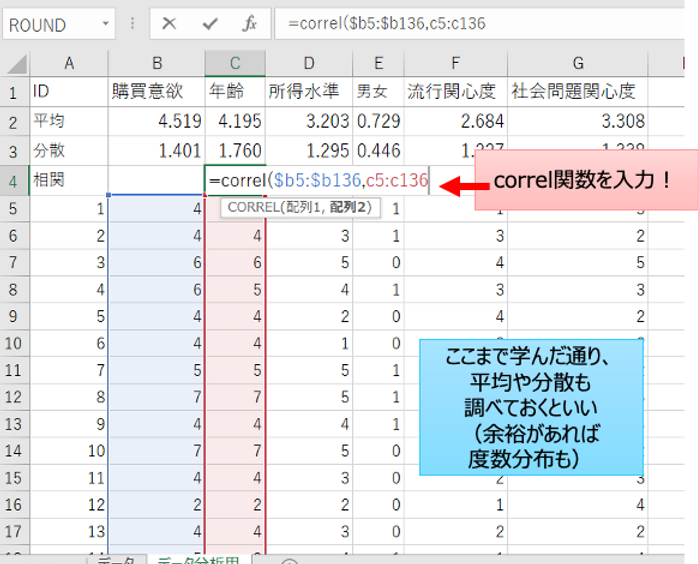
例えば先ほどの、この購買意欲と年齢や性別や所得水準などが関係しているんじゃないのかなというデータでやってみます。皆さんが実施するときも、Yにする列を、左側に置いて固定するというのをおすすめします。そして、右側にXの候補を並べていく。
correl関数に、まずYにする列を入力する。その隣に、Xになる列を入力する。同じ行を指定してあげることが大切です。
ちなみに、この上の図をぱっと見てお気づきになられた方もいると思うんですけ、私はいつも平均と分散も測定するのを習慣づけています。こういう分析をするときには、平均・分散がどういう状態なのかを頭に入れておくのが基本です。その上で、この2つの変数がどう関係してるんだろか、と理解を深めていくことになります。
もちろんあなたに余裕があれば、度数分布なども作っておくと、ベターだと思います。
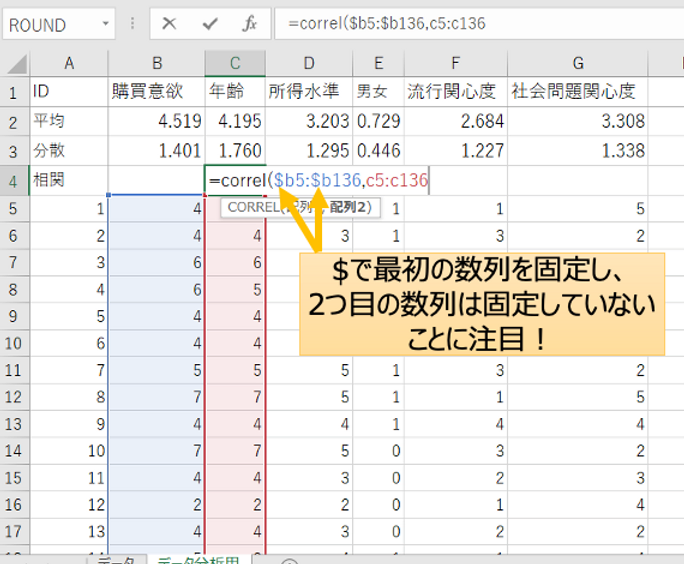
改めて、このcorrel関数に戻りましょう。また少し逸れますが、このドルマーク($)が実はとても便利です。$は、コピー・ペーストしたときに、その部分は固定することを意味します。
この$での固定をしない場合、コピー・ペーストをしたときにエクセルが気をきかせて1個ずつずらしてくれます。そうやって、別の行にも同じ処理をしてくれる便利機能ではあるのですが、今回は「Yとする行は固定したい」わけです。ですので、固定したい部分の前に$を置くわけです。
一方で、右側のC列の方は固定してないですよね。こちらは、コピー・ペーストするたびに、一つずつ参照する列がずれるため、隣の列を計算していくことができます。
このような意味で、まずこのYの方、結果の方を$で固定しておきましょう。そして右側の方、Xの方原因側の方をどんどんどんどん横にスライドしていけばペーストできるようにしておくといいでしょう。
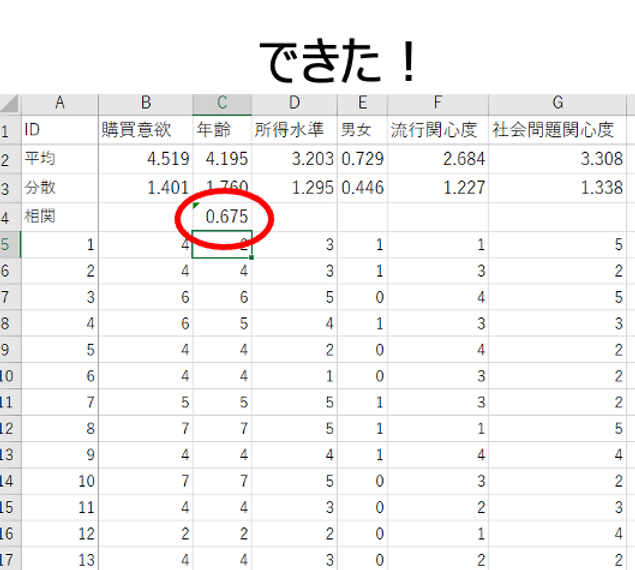
ここまでやりまして、エンターキー押してもらうと、相関が出てきます。今回の私のデータでは、0.675という相関が出てきました。正直0.675の相関というのはめちゃくちゃに大きい数字です。
相関係数から見えてくる
購買意欲と年齢というものが0.675という数字で相関しているということは、基本的にこの商品は、購買意欲が高い人は、シニア層の人、年齢が上がっていくと購買意欲が高まっていくということで、基本的にシニアの人をターゲットにしてる商品なんだなということがここで見えてくるわけです。
他の数字とも相関係数を見ていく
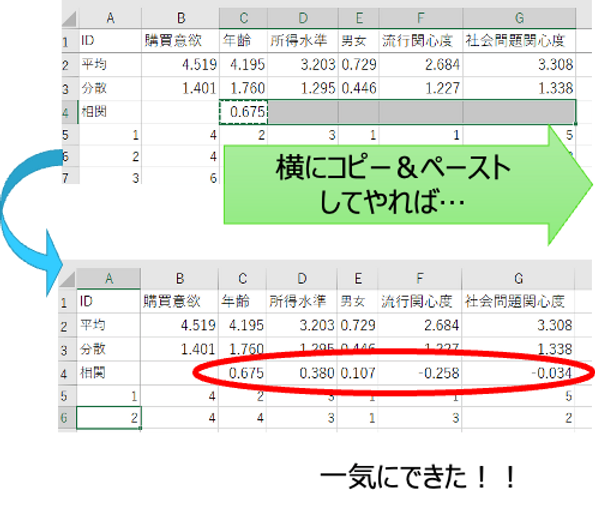
で、先ほども言ったようにこれを1個できたら、あとはもうコピー・ペーストする。そうすると一気にこんな感じにD列E列F列G列についても、ぱっと一気に出来上がっていくことになります。
数字を見て特徴を解釈する
とはいえです。ここまでの過程は、大きな会社の中であれば、若手の人だったりだとか、データアナリストさんだったりだとか、外注した人がやってくださる。
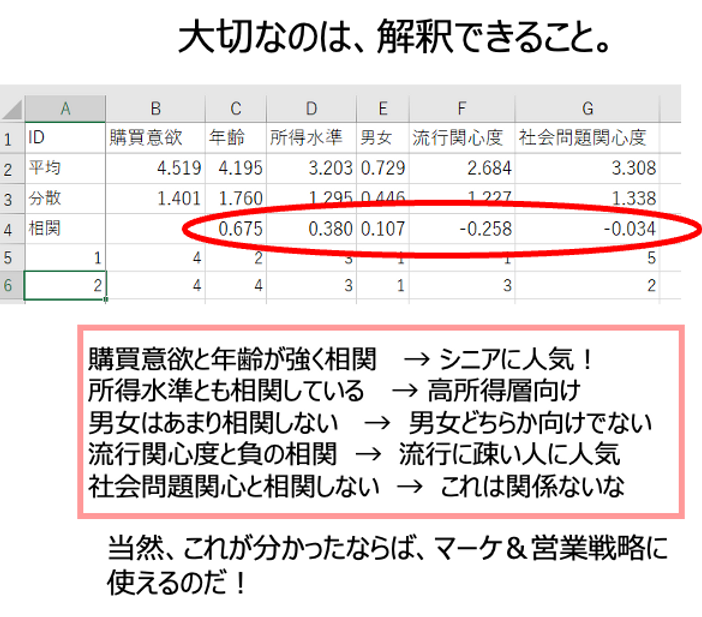
ビジネスパーソンとして大切になってくるのは、この数字を見て解釈ができることです。どうですか、皆さん、この購買意欲との各種数値との相関係数、この値を見て、あなたならどういう特徴をこの商品についてつかむことができるでしょうか?
相関するもの
購買欲と年齢層というものが強く相関していることは、シニアに人気な商品なんだなということ。また、所得水準とも相関していることは、高所得者向けの商品なんだなということが見えてくるわけです。
相関しないもの
また、男女は0.1ということでほとんど相関していない。男性向けが女性向けということはなくて、両方向けなんだなということになります。
また流行関心度に関してはー0.25ということで、マイナスの相関になっております。となってくると、これはむしろ、あんまりすごい流行感度が高い人向けではなくて、良いものを長く使うような感じの人に売れているのかな、ということが分かってくるわけです。少なくとも流行にはあまり敏感ではないようなタイプの人に人気の商品だということになってくる。
そして最後に社会関心度は、全く相関していないということで、これは関係ないんだなということが見えてくるわけです。
解釈し活用する
何が言えるのかといえば、当然これらの情報が、結果、事実として見えてきたならば、マーケティング営業戦略の大変重要な参考になるわけです。どういうターゲットに、どういう訴求の仕方をしていくのか、それがこの分析から見えてくる。
皆さんぜひこの相関というものもあなたの武器にしていただきたいなと思ってます!
ここから先は若干この相関というものを使っていくにあたって、アドバンストな話ということで、使っていく実務の中でいくつか注意すべき点があるので、これもこれから先もちょっとだけ学んでいたけど嬉しかったりします。

相関係数はどれくらいあると「高い」のか?
まず第1に相関の高さっていうのは、どれくらいあると高いと見えるのかということです。例えばご質問としてはこんなのを頂戴することが多いです。
「うちの会社の顧客満足度とアフターサービス品質の相関が0.3でした。これは高いのですか?」
0.3っていまいちじゃないんですか?という問いなのですが、学者的な答えは0.3の相関というのはめちゃくちゃ高いです。この顧客満足度っていうのは、森羅万象いろんなものが作用するわけですよ。何といってもまずその製品そのものが与える影響がありますし、価格が高いと不満も高まってきますし、顧客ライフスタイルなんかも作用する。いろんなことが作用する中で、顧客アフターサービスだけで0.3も影響力はあるんだとしたら、あなたの会社のアフターサービス部門はすごい優秀だということになります。

はっきり数字で目に取れるぐらい、アフターサービスが良いと結果がいいんですとなってるんだとすると、これは誇っていい数字です。それはまた、手を抜いたとすればはっきりマイナスの影響が出るということでもあります。アフターサービスしっかりやりましょうねというエビデンスとしては、非常に強いものだと言えるでしょう。
相関が0.8以上あったら相関しすぎておかしい
そして注意点第2は、逆に言うとこの社会科学分野で、特に経営や経済の事象を取り扱うにあたって、相関が0.8とか0.9もあったら、それは分析がミスっていると思うべきです。

例えばこういう状況です。
この会社のことが好きですか、というのを5段階で問い、またこの会社が商品買いたいですかというのも5段階評価でデータとして取りました。
その相関がなんと0.8もありました。
この二つの質問というのは、おそらく同じものを計っています。会社が好きだという事、会社の商品を買いたいかということ。会社を好きになる度合いを高めれば商品を買ってくれる、まあそれは事実でしょうが、当たり前の関係です。
数値が高過ぎたら、それは「異なる2つの事象の関係を見ている」と考える前に「同じものを別の表現で聞いているに過ぎない」という可能性を疑うべきです。森羅万象が作用する社会科学の中で、0.8とか0.9という相関はまずあり得ません。頭ん中で、これって同じこと言ってないかな、これってちゃんと原因と結果になってるかな、と考える。たいてい、どっちが原因でどっちが結果とも言えない。それはすなわち、渾然一体として同じ事象の別の側面を測っていたりするわけなのです。
見かけ上の相関
そして最後に、見かけ上の相関という問題。

例えば、毎日の売上高商品の売れ筋をチェックしていって、あるコンビニにおいては、ホッカイロが売れる日っていうのは、ホットコーヒーの出荷も伸びるんだということがわかった。
なるほど、ホッカイロを買うお客さんって、ホットコーヒーも買うんだな、ということでは、ないですよね。皆さんもお分かりですよね、不思議でも何でもない。単にそれは寒い日だからです。数字上、ホッカイロと缶コーヒーはセットで売れるように見えるけれども、寒い日だから両方を買っているに過ぎない。背後に、XとY以外の、第3の要因が作用しているわけです。
相関係数とか、そもそも統計分析というのは、数字ではっきり出てきてしまうがゆえに数字に踊らされがちになる。皆さんに気をつけていただきたいのは、頭できちんと原因と結果を考えることです。
そうした点に気をつけていただきながらも、この相関係数というのは本当に使いやすい指標です。何といっても、エクセルでぱっと出て、-1から1までの値で評価値を返してくれる。本当に自分で簡単に出来るものですから、ぜひこれも皆さんの技術にしてもらいたいと願っております。
著者・監修者
-

1982年生。経営学者/やさしいビジネススクール学長/YouTuber/経済学博士/関東学院大学 特任教授/法政大学イノベーション・マネジメント研究センター 客員研究員
詳しい講師紹介はこちら website twitter facebook youtube tiktok researchmap J-Global Amazon
専門は、経営戦略論・イノベーション・マネジメント、国際経営。
「アカデミーの力を社会に」をライフワークに据え、日本のビジネス力の底上げと、学術知による社会課題の解決を目指す。
「やさしいビジネススクール」を中心に、YouTube・研修・講演・コンサル・著作等で経営知識の普及に尽力中。


コメント